ContractionPPO: Certified Reinforcement Learning via Differentiable Contraction Layers

Abstract

Legged locomotion in unstructured environments demands not only high-performance control policies but also formal guarantees to ensure robustness under perturbations. Control methods often require carefully designed reference trajectories, which are difficult to construct in high-dimensional, contact-rich systems like quadruped robots. In contrast, Reinforcement Learning (RL) directly learns policies that implicitly generate motion, and uniquely benefits from access to privileged information, such as full state and dynamics during training, that is not available at deployment. We present ContractionPPO, a framework for certified robust planning and control of legged robots by augmenting Proximal Policy Optimization (PPO) RL with a state-dependent contraction metric layer. This approach enables the policy to maximize performance while simultaneously producing a contraction metric that certifies incremental exponential stability of the simulated closed-loop system. The metric is parameterized as a Lipschitz neural network and trained jointly with the policy, either in parallel or as an auxiliary head of the PPO backbone. While the contraction metric is not deployed during real-world execution, we derive upper bounds on the worst-case contraction residual and show that these bounds ensure the learned contraction metric generalizes from simulation to real-world deployment. Our hardware experiments on quadruped locomotion demonstrate that contraction augmented PPO enables robust, certifiably stable control even under strong external perturbations.

ContractionPPO Architecture

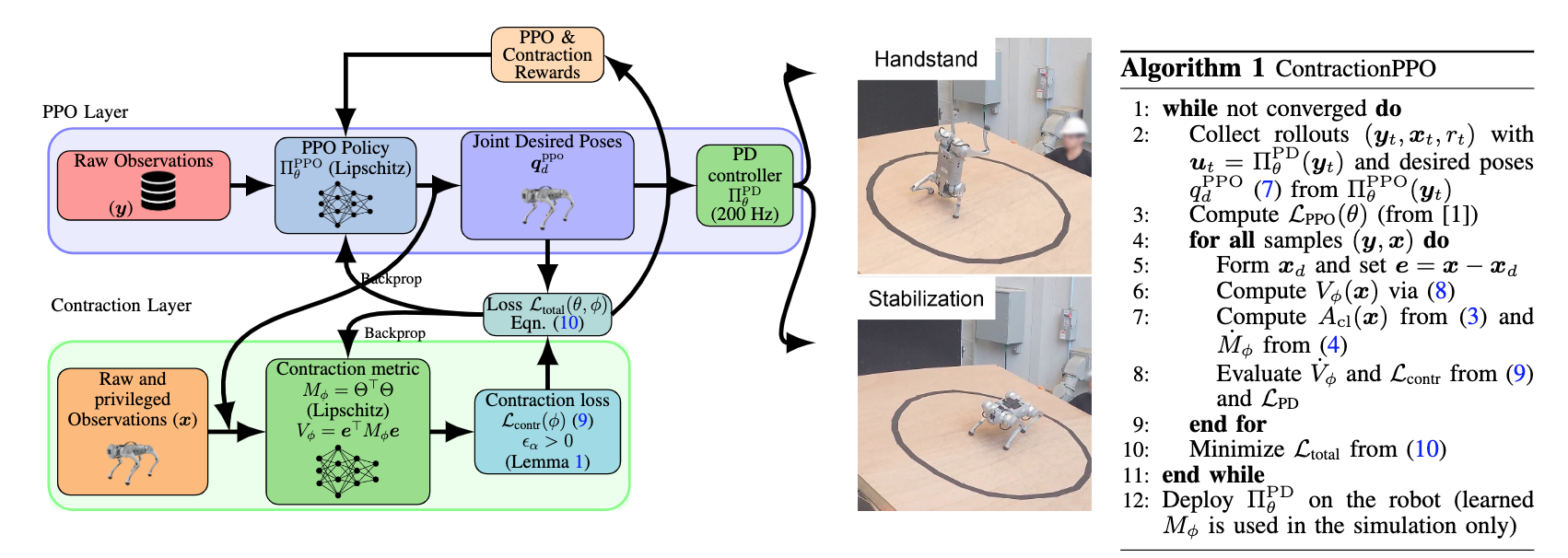
Architecture of ContractionPPO. The PPO policy processes raw observations $\mathbf{o}$ and outputs desired joint poses $\mathbf{x}_d$, which are executed by a low-level PD controller. In parallel, the contraction metric MLP $M_\phi$ receives privileged and raw observations $\hat{\mathbf{x}}$ and outputs a positive definite metric $M_\phi = \Theta^\top \Theta$. The contraction loss is evaluated using the Lyapunov condition $\dot{V} + \alpha V \leq -\epsilon_\alpha$, where $\alpha$ specifies the desired contraction rate and $\epsilon_\alpha$ quantifies the approximation margin between the learned value function $V_\phi$ and the true contraction Lyapunov function $V$. A larger $\alpha$ leads to faster convergence guarantees but also requires a larger $\epsilon_\alpha$, making optimization more challenging. This joint training setup ensures that the policy not only maximizes task reward but also satisfies certifiable incremental stability guarantees during locomotion.

ContractionPPO Deployment

Comparisons with Baseline Methods

ContractionPPO

TumblerNet

Rapid Motor Adaptation

PPO

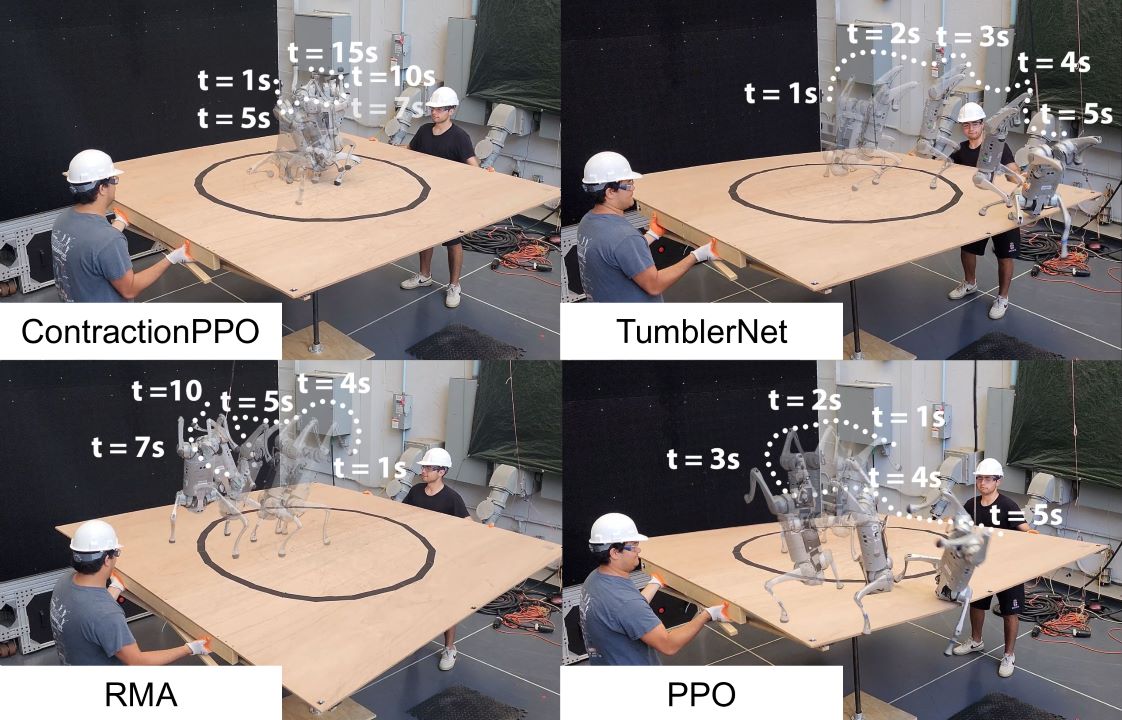
Comparison of trajectories for quadruped handstand using ContractionPPO (ours), TumblerNet, RMA and PPO where robots (for all baseline algorithms) were trained with identical reward functions that encourage remaining close to their initial position. While PPO, TumblerNet and RMA leaves the region and ultimately fails to remain on platform, ContractionPPO guarantees that the robot lie inside the circle (marked in black). This illustrates the core advantage of our approach i.e., provably stable and robust behavior.

Wind Experiments

Wind Speed: 4.8m/s

Wind Speed: 6.4m/s

Wind Speed: 8.0m/s

Wind Speed: 9.6m/s

*Wind disturbances were never seen during training

Quadruped trajectories during handstand under wind disturbances of varying magnitudes. As the disturbance intensity increases, transient deviations from the initial position become more evident. Note that ContractionPPO was never trained on external disturbances. Despite this, ContractionPPO policy ensures bounded trajectories and lies inside the circle marked by the black curve. This highlights the robustness and incremental stability guarantee of ContractionPPO, even under strong external perturbations.